Use Tensorflow to implement the form of linear support vector machine as an "application-oriented tutorial for Tensorflow"
This article is intended to be an "application-oriented tutorial" for TensorFlow by implementing a linear support vector machine (LinearSVM). While using MNIST as a tutorial project is almost a convention, I always feel like copying such examples and find them somewhat redundant. So, I decided to manually implement a LinearSVM.
Before diving into the implementation, let's briefly introduce the LinearSVM algorithm (for more details, refer to this resource).
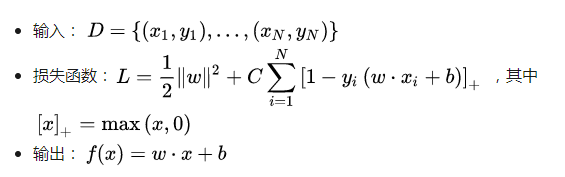
Now, let's discuss some key ideas in TensorFlow:
The core of TensorFlow is that it allows you to build a "Graph," where all you need to do is add elements to this graph. The basic elements include constants, variables (trainable), and non-trainable variables.
Since machine learning algorithms often involve minimizing a loss function, TensorFlow encapsulates the "minimize loss" step. You just need to express the loss in the graph and call the corresponding function to update all trainable variables.
When implementing LinearSVM, we will explain the third point later, but here we focus on the second. Let's first look at how to define the three basic elements and perform operations like addition, subtraction, multiplication, and division. (It's worth noting that in TensorFlow, variables in the graph are often referred to as "Tensors," so TensorFlow can be understood as "Tensor's flow." Note: A Tensor is called a tensor, which has mathematical significance; however, if you're not doing research, you can treat it as a high-dimensional array.)
```python
import tensorflow as tf
# Define constants with data type float32 for GPU computation
x = tf.constant(1, dtype=tf.float32)
# Define a trainable variable
y = tf.Variable(2, dtype=tf.float32)
# Define an untrainable variable
z = tf.Variable(3, dtype=tf.float32, trainable=False)
X_add_y = x + y
Y_sub_z = y - z
X_times_z = x * z
Z_div_x = z / x
```
Additionally, TensorFlow supports most NumPy methods, though the interface may differ slightly. For example, the "sum" operation:
```python
# Initialize a tensor from a NumPy array
x = tf.constant(np.array([[1, 2], [3, 4]]))
# TensorFlow equivalent of np.sum
axis0 = tf.reduce_sum(x, axis=0) # Results in [4, 6]
axis1 = tf.reduce_sum(x, axis=1) # Results in [3, 7]
```
Finally, to extract values from the graph, we need to define a Session. Think of the relationship between Graph and Session as follows: the Graph defines a set of "operation rules," while the Session "executes" these rules. During execution, the Session may perform three tasks:
- Extract desired intermediate results.
- Update all trainable variables (if the algorithm includes parameter updates).
- Provide specific values to placeholders defined in the operation rules.
To get the result of an operation, use `tf.Session().run()`:
```python
x = tf.constant(1)
y = x + 1
z = y + 1
print(tf.Session().run(y)) # Outputs 2
print(tf.Session().run([y, z])) # Outputs [2, 3]
```
A common mistake when using Variables is forgetting to initialize them before running the session. For example:
```python
x = tf.Variable(1)
print(tf.Session().run(x)) # This will raise an error
```
Correct approach:
```python
x = tf.Variable(1)
with tf.Session().as_default() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run(x)) # Correctly outputs 1
```
Now, moving on to the implementation of LinearSVM. From the previous discussion, the key is to express the loss function. Here’s a simplified version of the loss function used:
$$ \text{cost} = \sum_{i=1}^N \max(1 - y_i \cdot (w \cdot x_i + b), 0) + \frac{1}{2} \|w\|^2 $$
Here’s the code for the `TFLinearSVM` class:
```python
import tensorflow as tf
from Util.Bases import ClassifierBase
class TFLinearSVM(ClassifierBase):
def __init__(self):
super(TFLinearSVM, self).__init__()
self._w = self._b = None
self._sess = tf.Session()
def fit(self, x, y, sample_weight=None, lr=0.001, epoch=10**4, tol=1e-3):
if sample_weight is None:
sample_weight = tf.constant(
np.ones(len(y)), dtype=tf.float32, name="sample_weight"
)
else:
sample_weight = tf.constant(
np.array(sample_weight) * len(y), dtype=tf.float32, name="sample_weight"
)
x, y = tf.constant(x, dtype=tf.float32), tf.constant(y, dtype=tf.float32)
self._w = tf.Variable(np.zeros(x.shape[1]), dtype=tf.float32, name="w")
self._b = tf.Variable(0., dtype=tf.float32, name="b")
y_pred = self.predict(x, True, False)
cost = tf.reduce_sum(
tf.maximum(1 - y * y_pred, 0) * sample_weight
) + tf.nn.l2_loss(self._w)
train_step = tf.train.AdamOptimizer(learning_rate=lr).minimize(cost)
self._sess.run(tf.global_variables_initializer())
for _ in range(epoch):
if self._sess.run([cost, train_step])[0] < tol:
break
def predict(self, x, get_raw_results=False, out_of_sess=True):
rs = tf.reduce_sum(self._w * x, axis=1) + self._b
if not get_raw_results:
rs = tf.sign(rs)
if out_of_sess:
rs = self._sess.run(rs)
return rs
```
One important note is that using `Session` to extract intermediate results can have overhead. It's best to avoid opening sessions unnecessarily, especially when dealing with large graphs.
At the end, let's look at the use of `Placeholder` in TensorFlow. Although our current implementation works, it may have memory issues. To address this, a common practice is to use batch training, which involves feeding small batches of data each time. Placeholders allow us to define "unfixed" data during the training process.
```python
# Define a placeholder for input data
x = tf.placeholder(tf.float32, [None, 2])
# Define a numpy array
y = np.array([[1, 2], [3, 4], [5, 6]])
# Define a simple operation
z = x + 1
# Run the session with feed_dict
print(tf.Session().run(z, feed_dict={x: y})) # Outputs [[2, 3], [4, 5], [6, 7]]
```
Using placeholders makes the model more flexible and efficient, especially when working with large datasets. In our current implementation, the lack of placeholders may lead to performance issues, especially when repeatedly calling the `predict` method. This is something to consider for future improvements.
Overall, this was a brief introduction to TensorFlow, focusing on practical implementation rather than theoretical depth. If there are any unclear parts, feel free to ask!
Shaanxi Xinlong Metal Electro-mechanical Co., Ltd. , https://www.cnxlalloys.com